本帖最后由 dj2436 于 2025-9-16 21:46 编辑
脑电信号(EEG)包含丰富的神经活动信息,但原始波形数据维度高、噪声多。特征提取是将EEG时序信号转换为简洁、易处理的特征向量的关键步骤。在脑机接口(BCI)系统中,这些特征常用于机器学习分类器以识别认知状态或控制外部设备。例如,通过提取功率谱特征可以区分不同睡眠阶段和意识水平,通过非线性复杂度特征可以监测麻醉深度或癫痫活动。因此,系统性地了解EEG各类特征的定义、计算方法和应用场景,对于BCI研究人员快速入门具有重要意义。在后续的介绍中,我们假设信号长度为N,采样率为fs。
一. 时域特征
EEG信号的本质是一个时间序列,因此最直观的特征提取方式就是直接在EEG信号本身进行提取。通过这一方式提取到的特征被称为时域特征,常见的时域特征有以下几种:
1. 均值(Mean):衡量信号的平均电位。定义为:
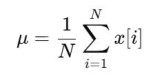
EEG信号的均值反映了基线电位水平,一般在零附近。 2. 方差(Variance):描述信号离散程度。定义为:
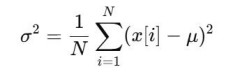
方差值大表示信号幅度波动剧烈,可用于区分脑电活动强度差异。 3. 均方根(RMS, Root Mean Square):衡量信号功率大小的一种表示。定义为:
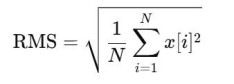
均方根值大代表信号整体能量较大。 4. 峰峰值:信号最大值与最小值之差。定义为:
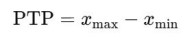
常用于表征EEG振幅范围,如评估脑电高幅振荡事件。 5. 偏度:描述信号分布的对称性。定义为:
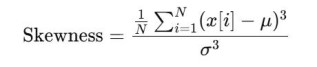
偏度为正表示右偏(长右尾,更多低值),负表示左偏(长左尾)。EEG偏度常用于检测异常尖峰或不对称波形。 6. 峰度:描述分布“峰值”特征。定义为:
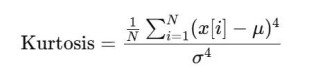
峰度表示信号集中在均值附近且存在长尾。在EEG中,高峰度通常对应大量极值出现,可能与癫痫尖峰或事件相关电位(ERP)有关。 7. 零交叉率(ZCR):信号跨越零轴的频率,能够间接反映频率。定义为:
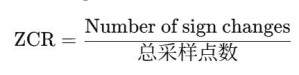
ZCR可看作信号“嘈杂度”指标,频率含量高的信号ZCR也高。例如在睡眠分期中,深睡时EEG低频多、ZCR低;清醒时高频成分多、ZCR高。 8. 过零平均间隔(MZCI):与ZCR类似,可以看作它的倒数,定义为:

同样反应的是频率含量。 以上就是常见的时域特征,前四个可以记作常见的统计特征,后四个可以归类为波形形态特征。
二. 频域特征
观察EEG信号的另一种重要方式是通过频谱图,因为EEG信号可以看作由不同频率成分组成,每个频率有不同的强度,通过频谱分析可以更好的分析信号对应时段大脑的状态。想要将信号中的频率成分分离出来并直观展示,在EEG信号处理领域常用的方法是离散傅里叶变换(DFT)和功率谱密度(PSD)图。
1. 离散傅里叶变换(DFT):将离散的时域信号转换到频域,用于表示信号包含哪些频率成分。定义为:
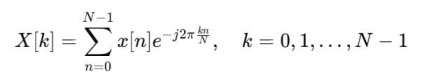
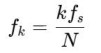
通过DFT能够得到N个不同的频率分量,均为复值,需要注意的是得到的结果是与信号强度相关的。 2. 功率谱密度(PSD):描述信号的功率随频率的分布,单位通常是 μV²/Hz。定义为:
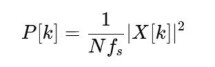
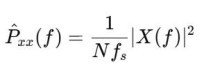
但直接使用DFT对整个信号序列进行处理,然后计算PSD容易出现误差大的问题,比如局部的异常值经过DFT会对所有频率分量产生影响。因此更常用的方法是Welch方法,它的具体计算步骤为:1)将信号分成有重叠部分的段;2)加窗,使用窗函数让信号两端平滑的过渡到0;3)每段分别进行DFT;4)对各段的DFT结果计算PSD然后求平均。 频域的常用特征一般是基于计算得到的PSD进行计算的,常见的有以下几种:
1. 总功率:刻画EEG信号在整个频段上的能量总和,不过这个范围一般根据不同的任务有所不同,比如在睡眠领域我们关注的一般是0.5-30Hz范围内的频率信息。定义为:
2. 频带比值:用于刻画某一频段的功率占比,用于判断信号由哪个频段主导。定义为:
3. 频带间比值:描述不同频带间的能量关系。定义为:
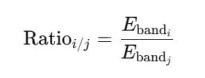
一些比值常作为特征,用于注意力评估和病理状态检测。 4. 谱熵(Spectral Entropy):度量功率谱分布复杂度的熵指标。定义为:
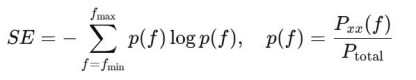
谱熵越大,表示能量分布越分散;谱熵越小,表示能量集中在狭窄频带。在BCI中,谱熵可用于监测麻醉深度和睡眠状态零交叉率(ZCR):信号跨越零轴的频率,能够间接反映频率。
三. 时频域特征 在频域特征中我们介绍了DFT,易知这一方法是全局的,与信号长度紧密相关,但使用DFT方法无法让我们知道某一时刻某一频率的具体信息,为了将时域信息融入频域,常采用时频域变换的方法,最常用方法有短时傅里叶变换(STFT)和小波变换(WT)。
1. 短时傅里叶变换(STFT):对每一个时刻进行采用时间窗计算频谱,将信号映射到时间-频率平面。定义为:
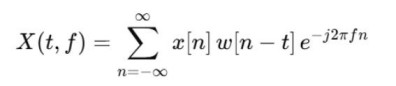
需要注意的是,STFT是固定时间窗大小的,因此要选择合适的值在时间分辨率和频率分辨率之间进行权衡。常用的是长度为1-4s,50%重叠的窗。 2. 小波变换(WT):小波变换和STFT的作用类似,但它不存在STFT中的时频分辨率权衡的问题,它可以根据频率自适应调整时间窗的大小。定义为:

但因为在BCI领域,我们需要实时性、效率高、特征提取方便的方法,因此更常使用的是离散小波变换(DWT),它的本质是一个滤波器组,原理是:通过滤波器组将EEG信号分解成不同的频率子带,使用低通滤波保留低频成分,高通滤波保留高频成分,然后对低频成分重复操作。 基于变换得到的结果我们可以计算下面的时频域特征:
1. 子带能量:它定义为:
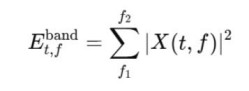
对时频图中的每个频段计算能量,可以从时间维度观察能量的变化。 2. 时频熵:它定义为:
类似谱熵,但加入了时间维度。
四. 复杂度特征
复杂度特征用刻画EEG信号的非线性和混沌性质,常用于区分意识状态和病理变化,我们前面已经给出了谱熵的概念,这里介绍更多常见的复杂度特征。
1. 近似熵(ApEn):衡量样本序列模式相似性。定义为:
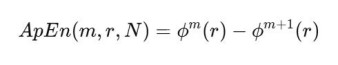
其中
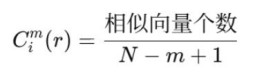
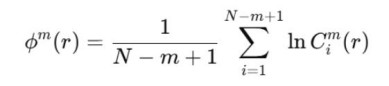
但近似熵存在自匹配、序列短时不稳定、以及受阈值影响(定义向量相似的阈值)的缺点。 2. 样本熵(SampEn):同样时衡量样本序列模式相似性的特征。定义为:
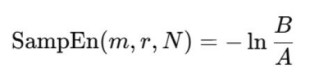
这里A、B分别是m+1、m长度下向量相似的对数。相比近似熵,样本熵优化掉了自匹配,并直接采用概率比进行计算,但它同样收到阈值的影响。 3. Lempel–Ziv 复杂度(LZC):计算LZC前需要先对信号序列进行符号化(常用中位数二值化),之后扫描整个序列,对于未出现过的字符串进行计数,之后计算:
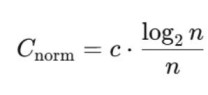
我们记右侧为k,需要对计数乘k的原因在于,序列越长,LZ复杂度值会自然变大,最复杂的序列(完全随机)会在长度n时,最多出现大约1/k个新模式。 4. Hjorth 参数:使用方差、离散一阶差分、离散二阶差分,采用递进的视角统计信号的变化程度。定义了活动度、移动度、复杂度分别为:
5. 分形维度(FD):用于衡量信号曲折/自相似的程度。它的最常用计算方法是Katz方法:
其中d是信号中起点到最远点的距离,L是信号曲线总长度。这种方法最简单,适合EEG信号处理对实时性的要求。
以上各类特征涵盖了EEG信号处理中常见的核心指标。它们在BCI任务中可用于区分不同的脑电状态,如睡眠分期、意识水平、情绪状态和运动想象等。不同特征反映EEG信号的不同属性,例如时域统计量侧重幅值特征,频域功率反映节律强度,时频特征结合时变信息,而复杂度指标捕捉信号的非线性和随机性。根据具体应用需求,可综合使用多类特征以提高识别性能。
参考文献:
[1] Singh A K, Krishnan S. Trends in EEG signal feature extraction applications[J]. Frontiers in artificial intelligence, 2023, 5: 1072801.
[2] Boonyakitanont P, Lek-Uthai A, Chomtho K, et al. A review of feature extraction and performance evaluation in epileptic seizure detection using EEG[J]. Biomedical Signal Processing and Control, 2020, 57: 101702.
[3] Sun C, Mou C. Survey on the research direction of EEG-based signal processing[J]. Frontiers in Neuroscience, 2023, 17: 1203059.
|